二叉树
定义
二叉树的每个结点至多只有两棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。
二叉树的第i(在这里根结点为第一层)层至多有2^(i-1)个结点。
深度为k(根结点深度为1)的二叉树至多有(2^k)-1个结点。
示例
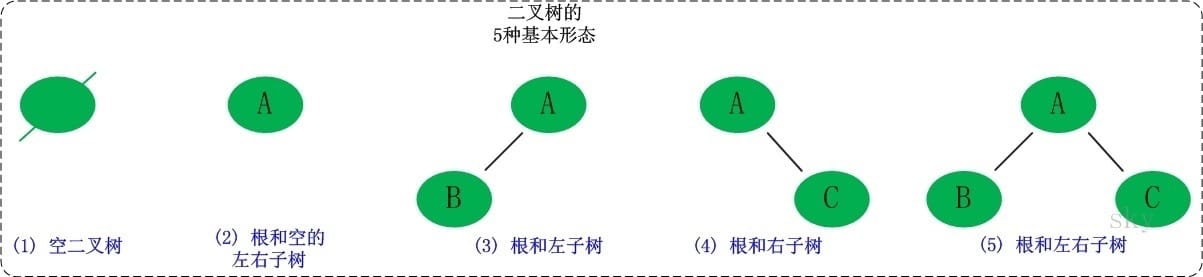
性质
(1) 在二叉树中,第i层的结点总数不超过2^(i-1);
(2) 深度为k的二叉树最多有(2^k)-1个结点,最少有k个结点;
(3) 对任意一棵二叉树,如果其叶子结点数为N0,而度为2的结点总数为N2,那么N0=N2+1;
树的遍历
前序遍历
前序遍历(Pre-Order Traversal)的访问顺序:根节点、左子树、右子树。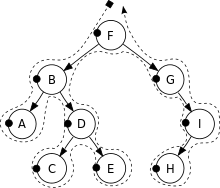
前序遍历结果:F, B, A, D, C, E, G, I, H.
中序遍历
中序遍历(In-Order Traversal)的访问顺序:左子树、根节点、右子树。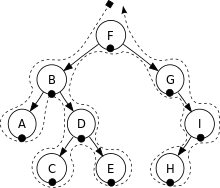
中序遍历结果:A, B, C, D, E, F, G, H, I.
后序遍历
后序遍历(Post-Order Traversal)的访问顺序:左子树、右子树、根节点。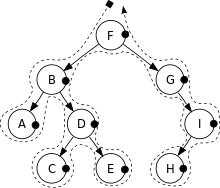
后序遍历结果:A, C, E, D, B, H, I, G, F.
满二叉树
定义
除叶子结点外的所有结点均有两个子结点,结点数达到最大值,所有叶子结点必须在同一层上。
性质
一棵深度为k的满二叉树具有如下性质:
(1) 叶子结点数为2^(k-1).
(2) 总结点数为(2^k)-1,即总结点数一定是奇数。
完全二叉树
定义
若一个二叉树深度为k,除第k层外,其它各层(1~(k-1)层)的结点数都达到最大个数,且第k层所有的结点都连续集中在最左边,这就是完全二叉树。
性质
完全二叉树除了具备普通二叉树的3种通用性质外还有以下2个特性。
(1) 具有n个结点的完全二叉树的深度为int(log2n)+1
(2) 给定N个结点,能构成h(N)种不同的二叉树
h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1);
二叉查找树
定义
又称为二叉排序树(Binary Sort Tree)或二叉搜索树。二叉查找树(Binary Search Tree)或者是一棵空树,或者是具有下列性质的二叉树:
(1) 若任意结点的左子树不为空,则左子树上所有结点的值均小于它的根结点的值。
(2) 若任意结点的右子树不为空,则右子树上所有结点的值均大于它的根结点的值。
(3) 任意结点的左、右子树也分别为二叉查找树。
(4) 没有键值相等的结点。
性质
中序遍历一个二叉查找树可以得到一个关键字的有序序列。
平衡二叉树
背景
我们知道,对于一般的二叉搜索树(Binary Search Tree),其期望高度(即为一棵平衡树时)为log2n,其各操作的时间复杂度O(log2n)同时也由此而决定。但是,在某些极端的情况下(如插入的序列是有序的时候),二叉搜索树将退化成单链表,此时,其操作的时间复杂度将退化成线性的,即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况,但是在进行了多次的操作之后,由于在删除时,我们总是选择将待删除节点的后继代替它本身,这样就会造成总是右边的节点数目减少,以至于树向左偏沉。这同时也会造成树的平衡性受到破坏,提高它的操作的时间复杂度。于是就有了我们下边介绍的平衡二叉树。
定义
平滑二叉树(Balanced Binary Tre)也叫AVL(来源于该数据结构的发明者Adelson-Velsky和Landis)树,它要么是一棵空树,要么是具有如下性质的二叉树:
(1) 任意结点的左右子树高度差的绝对值不超过1。
基本概念
平衡因子
某结点的左子树与右子树的高度差即为该结点的平衡因子BF(Balance Factor),在一棵平衡二叉树中,结点的平衡因子取值范围(-1,0,1),分别对应左低右高,左右等高,左高右低。
最小失衡子树
在新插入的结点向上查找,以第一个平衡因子的绝对值超过1的结点为根的子树成为最小不平衡子树。也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
左旋-右旋
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式,左旋 与 右旋 。
AVL树
AVL树是最早的自平衡二叉树,相比于后来出现的红黑树而言,它现在应用较少。
定义
一棵AVL树满足以下的条件:
(1) 它的左子树和右子树都是AVL树
(2) 左子树和右子树的高度差不能超过1
AVL 树是高度平衡的,频繁的插入和删除,会引起频繁的reblance,导致效率下降,但它的查找效率较高,适合于插入删除操作较少,查找较多的场景。
红黑树
红黑树(RBT-Red-Black Tree)不是高度平衡的,算是一种折中,插入最多两次旋转,删除最多三次旋转。
B树、B+树、B* 树
B树也是一种用于查找的平衡树,但是它不是二叉树。
B+树是B树的变体,也是一种多路搜索树。
B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针,将结点的最低利用率从1/2提高到2/3。
Trie树
Tire树称为字典树,又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
性质
(1) 根节点不包含字符,除根节点外每一个节点都只包含一个字符;
(2) 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串;
(3) 每个节点的所有子节点包含的字符都不相同;
应用
(1) 串的快速检索
给出N个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。
在这道题中,我们可以用数组枚举,用哈希,用字典树,先把熟词建一棵树,然后读入文章进行比较,这种方法效率是比较高的。
(2) “串”排序
给定N个互不相同的仅由一个单词构成的英文名,让你将他们按字典序从小到大输出。用字典树进行排序,采用数组的方式创建字典树,这棵树的每个结点的所有儿子很显然地按照其字母大小排序。对这棵树进行先序遍历即可。
(3) 最长公共前缀
对所有串建立字典树,对于两个串的最长公共前缀的长度即他们所在的结点的公共祖先个数,于是,问题就转化为求公共祖先的问题。